Shear layer rollup#

The shear layer rollup is a 2-dimensional ideal incompressible flow (Euler flow). And the external body force is zero.

The flow is in a periodic domain $Ω = [0, 2 π]^{2}$ , and components of the initial velocity $u^{0} = {[\begin{matrix} u^{0} & v^{0} \end{matrix}]}^{T}$ are

\begin{array}{r} u^{0} = {\begin{aligned} \tanh (\frac{y - \frac{π}{2}}{δ}) if y \leq π \\ \tanh (\frac{\frac{3 π}{2} - y}{δ}) else \end{aligned}, \end{array}

and

v^{0} = ϵ \sin (x),

where $δ = π / 15$ and $ϵ = 0.05$ .

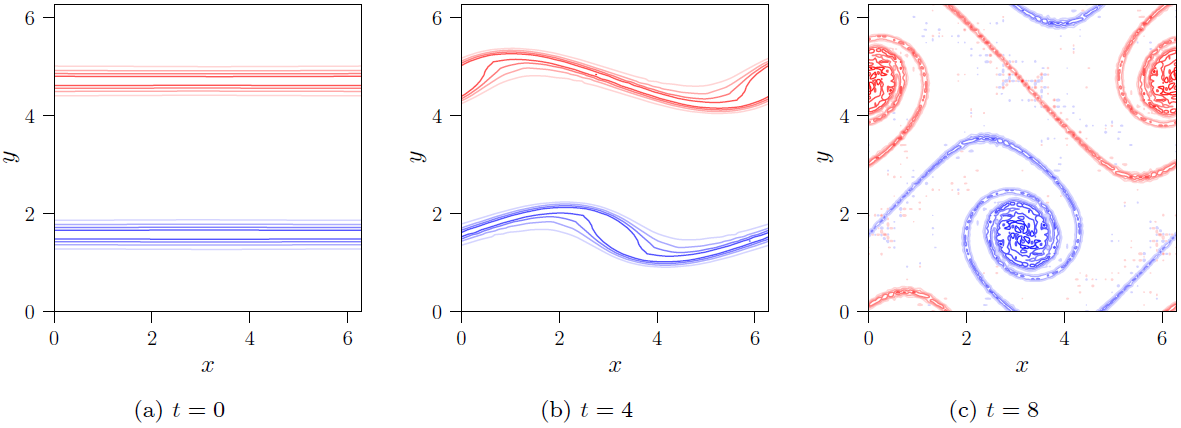
../../../_images/t048.png — Fig. 14 The vorticity field of the shear layer rollup flow at $t \in {0, 4, 8}$ with contour lines for ${\pm 1, \pm 2, \dots, \pm 6}$ .#

It is seen that two vorticity layers gradually roll up due to the initial perturbation in the velocity field.

For a phyem implementation of the shear layer rollup using the dual-field method introduced in [Dual-field NS, Zhang et al. JCP (2022)], click phyem_df2_slr.py.

↩️ Back to 🌊 Navier-Stokes equations.