Multi-crazy domain and mesh

The multi-crazy ones are like stacking multiple Crazy domain and mesh (blocks) together. The parameters are same to those of the crazy mesh except there is one additional, Ns, see:

crazy_multi(bounds=None, c=0, Ns=None, periodic=False)

Parameters:

boundslist, tuple, None, default=None

The bounds of the domain along each axis. When it is None, the code will automatically analyze the manifold and set the bounds to be \([0,1]^n\) where \(n\) is the dimensions of the space.

For example, the unit cube is of bounds = ([0, 1], [0, 1], [0, 1]).

cfloat, default=0.

The deformation factor. c must be in \([0, 0.3]\). When c = 0, the domain is orthogonal, and when c > 0, the space in the domain is distorted.

Nslist, None, default=None

Ns should be a list of \(n\) (the dimensions of the manifold) positive integers. It means along each axis, we will stack how many crazy meshes.

When it is None, the code will automatically analyze the manifold and then set Ns to be \([\underbrace{2, 2, \cdots}_{n}]\).

periodicbool, default=False

It indicates whether the domain is periodic. When it is True, the domain is fully periodic along all axes. And when it is False, the domain is not periodic at all.

Boundary units

Since the amount of regions is dynamic, its amount of boundary units is dynamic as well. They contain the boundary faces of these regions attached to the domain boundary. For example, when there are \(2 * 3\) regions/blocks, the complete set of boundary units is

>>> boundary_units_set = {
...     0: [1, 0, 1, 0],
...     1: [0, 1, 1, 0],
...     2: [1, 0, 0, 0],
...     3: [0, 1, 0, 0],
...     4: [1, 0, 0, 1],
...     5: [0, 1, 0, 1],
... }

Examples

We now generate a multi-crazy mesh in domain \(\Omega:=(x,y,z)\in[-1,1]\times[0,2]\subset\mathbb{R}^2\) of \(2 * 3\) crazy regions/blocks at \(c=0.3\). In each crazy block, we make \(5 * 3\) elements. The codes are

>>> ph.config.set_embedding_space_dim(2)
>>> manifold = ph.manifold(2)
>>> mesh = ph.mesh(manifold)
>>> msepy, obj = ph.fem.apply('msepy', locals())
>>> manifold = obj['manifold']
>>> mesh = obj['mesh']
>>> msepy.config(manifold)('crazy_multi', c=0.3, periodic=False, Ns=[2, 3], bounds=[[-1, 1], [0, 2]])
>>> msepy.config(mesh)([5, 3])
>>> mesh.visualize(saveto=None_or_custom_path)  
<Figure size ...

The multi-crazy mesh is visualized as

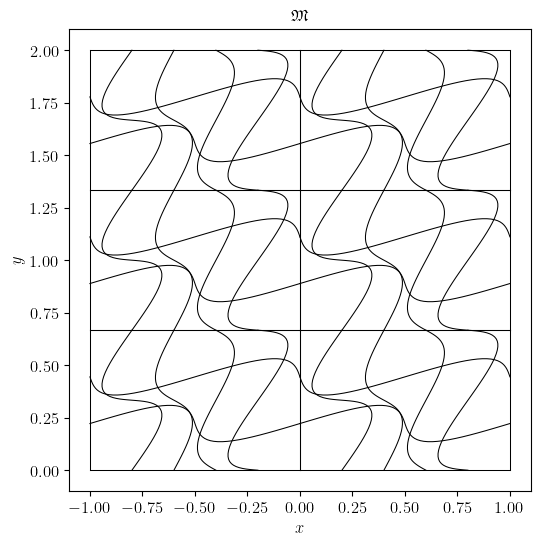
Fig. 9 The crazy mesh in \(\Omega=[-1,1]\times[0,2]\subset\mathbb{R}^2\) of \(2 * 3\) blocks at deformation factor \(c=0.3\). In each block, we have \(5 * 3\) elements.

↩️ Back to msepy domains and meshes.