Lid-driven cavity

The lid-driven cavity flow is a incompressible viscous flow.

In 2-dimensions, it is usually cast as follows. The domain is set to be \(\Omega=[0,1]^2\) with four infinite no-slip solid walls. The media is still initially. From time \(t=0\), the top wall, i.e. \(y=1\), moves left with a constant speed, i.e. the lid speed, \(\left.\boldsymbol{u}\right|_{\mathrm{lid}}=\begin{bmatrix}-1, 0\end{bmatrix}^\mathsf{T}\), and drives the viscous flow. The simulation stops when the flow becomes steady.

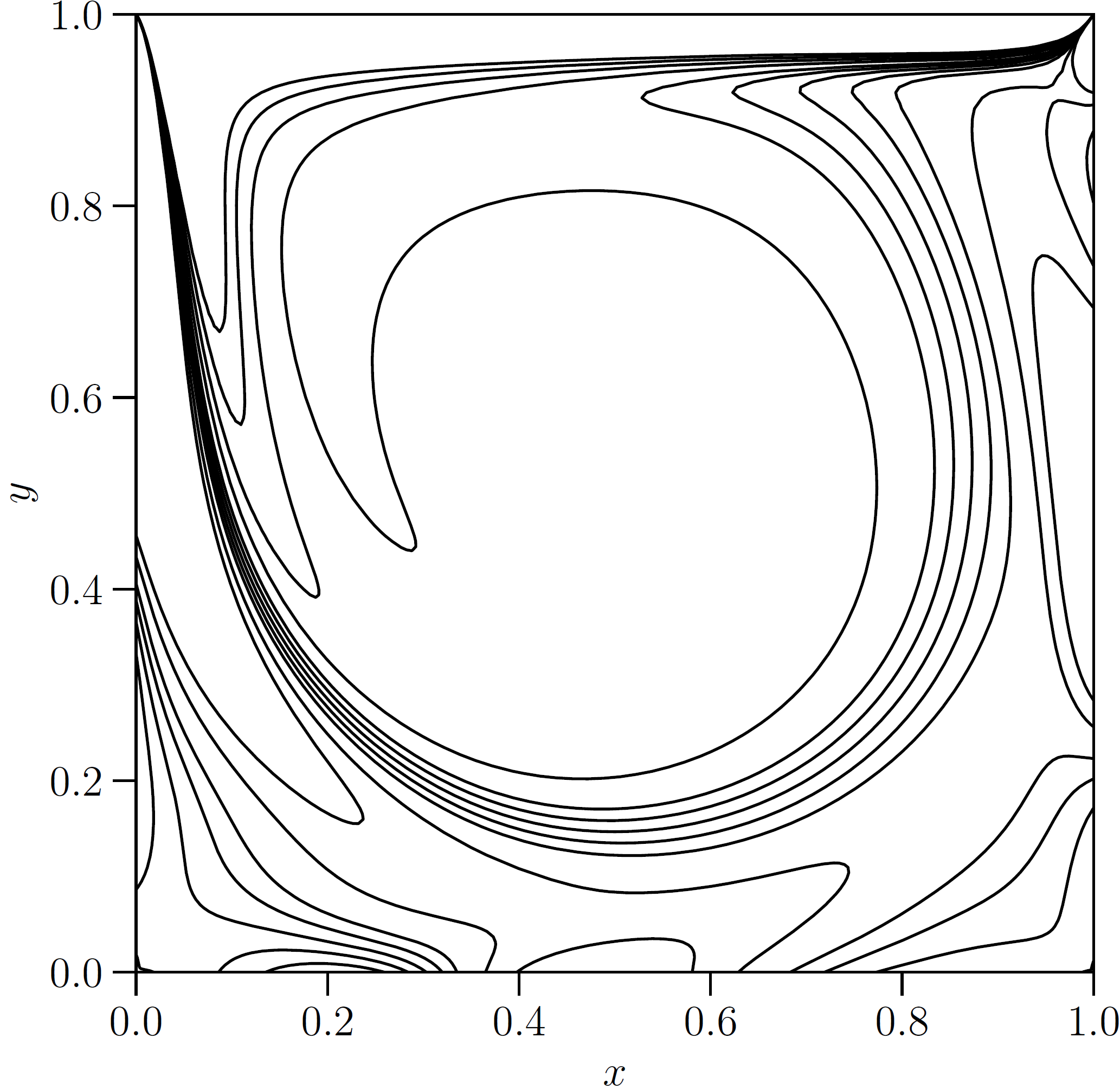
The steady case of \(\omega\) for the 2-dimensional lid-driven cavity flow.

For a phyem implementation of the normal dipole collision test case in Section 5.4 of [MEEVC, Zhang et al., JCP (2024)], click phyem_ldc.py.

↩️ Back to 🌊 Navier-Stokes equations.