Backward step#
The backward step is a mesh (or domain) in
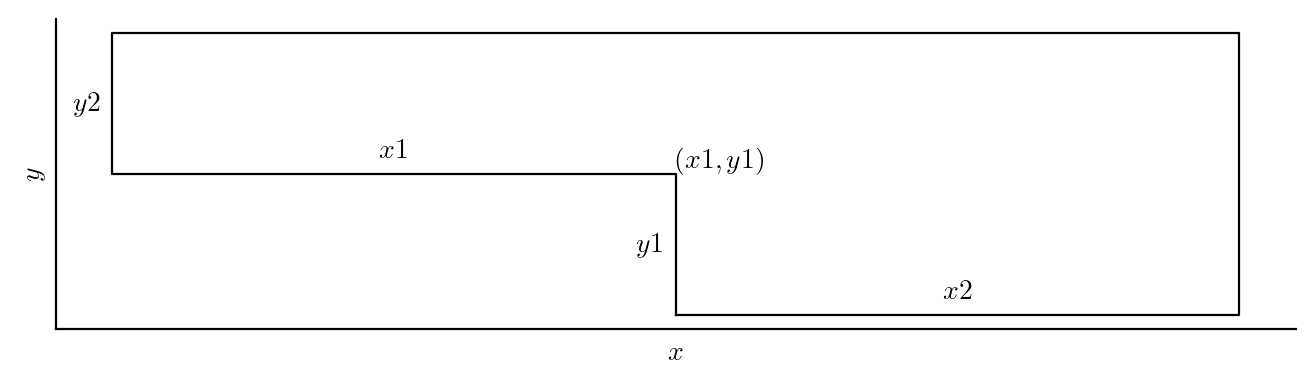
Fig. 1 The illustration of the backward step domain.#
When
- backward_step(x1=1, x2=1, y1=0.25, y2=0.25, z=None, periodic=False)[source]#
- Parameters:
- x1float, default=1
See the illustration.
- x2float, default=1
See the illustration.
- y1float, default=0.25
See the illustration.
- y2float, default=0.25
See the illustration.
- zfloat, None, default=None
When it is
None, it gives a two-dimensional domain. Otherwise,- periodicbool, default=False
When the domain is 3d, whether it is periodic along the
z-axis?
Boundary units#
The domain is divided into three regions,
region |
bottom-right region, |
region |
top-right region , |
region |
top-left region, |
Thus, for a 2-dimensional domain, it has 8 boundary units, i.e.,
>>> boundary_units_set = {
... 0: [1, 1, 1, 0],
... 1: [0, 1, 0, 1],
... 2: [1, 0, 1, 1],
... }
For example, for the bottom-right region 0, its left (0: [1, 1, 1, 0] in the set.
And a 3-dimensional domain, it has 8 + 6
(
>>> boundary_units_set = {
... 0: [1, 1, 1, 0, 1, 1],
... 1: [0, 1, 0, 1, 1, 1],
... 2: [1, 0, 1, 1, 1, 1],
... }
Examples#
3d#
Below codes will lead to a three-dimensional backward step mesh of
>>> ph.config.set_embedding_space_dim(3)
>>> manifold = ph.manifold(3)
>>> mesh = ph.mesh(manifold)
>>> msepy, obj = ph.fem.apply('msepy', locals())
>>> manifold = obj['manifold']
>>> mesh = obj['mesh']
>>> msepy.config(manifold)('backward_step')
>>> msepy.config(mesh)([5, 5, 5])
>>> mesh.visualize(saveto=None_or_custom_path_3)
<Figure size ...
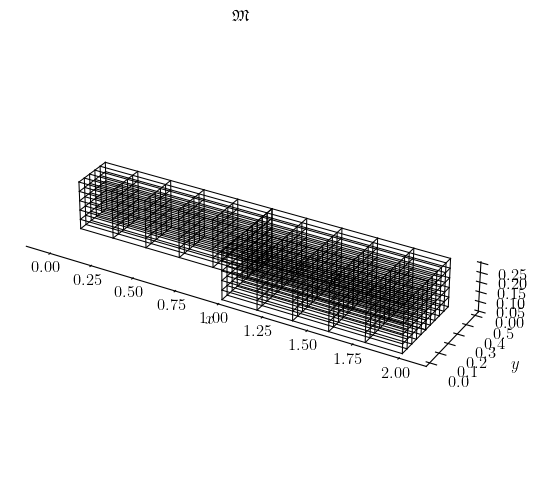
Fig. 2 The three-dimensional backward step mesh of
2d#
To make a two-dimensional backward step mesh of
>>> ph.config.set_embedding_space_dim(2)
>>> manifold = ph.manifold(2)
>>> mesh = ph.mesh(manifold)
>>> msepy, obj = ph.fem.apply('msepy', locals())
>>> manifold = obj['manifold']
>>> mesh = obj['mesh']
>>> msepy.config(manifold)('backward_step')
>>> msepy.config(mesh)([24, 6])
>>> mesh.visualize(saveto=None_or_custom_path_2)
<Figure size ...
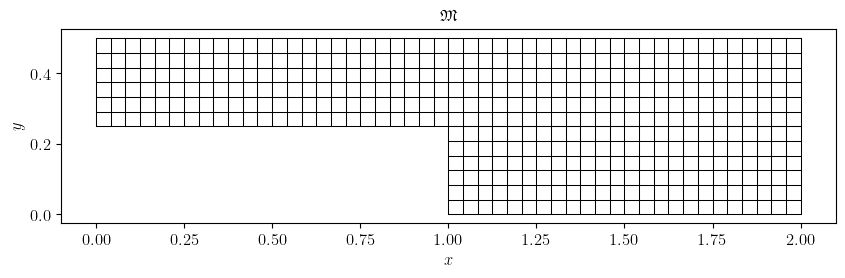
Fig. 3 The two-dimensional backward step mesh of
↩️ Back to msepy domains and meshes.

